Cette étude décrit le mouvement d’une “patte” d’un Hexapod PhanthomX AX Mark II, selon la convention de Denavit-Hartenberg.

Chaine cinématique d’une patte

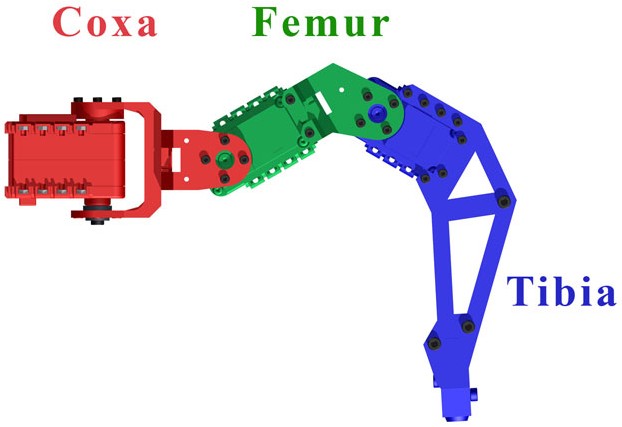
Chaque patte du robot est constituée de trois partie :

Coxa : Partie fixée au robot pour gérer le placement de la patte,
Femur : Partie intermedaire permettant de controler la hauteur de la patte,
Tibia : Partie permettant de gérer l’allongement de la patte.

Calcul du système de référence

Mise en place du MGS : 3R

3 rotations : $θ_{1} θ_{2} θ_{3}$
3 constantes : $l_{1} l_{2} l_{3}$

Tableaux de Denavit-Hartenberg

Paramètres	liaisons	axe
θ	$(x_{0}, x_{1}) = θ_{1}$	$\vec{z_{0}}$
d	$x_{0} / x_{1} = 0$	$\vec{z_{0}}$
α	$(z_{0}, z_{1}) = \frac{π}{2}$	$\vec{x_{1}}$
a	$z_{0} / z_{1} = l_{1}$	$\vec{x_{1}}$

Paramètres	liaisons	axe
θ	$(x_{0}, x_{1}) = θ_{1}$	$\vec{z_{0}}$
d	$x_{0} / x_{1} = 0$	$\vec{z_{0}}$
α	$(z_{0}, z_{1}) = \frac{π}{2}$	$\vec{x_{1}}$
a	$z_{0} / z_{1} = l_{1}$	$\vec{x_{1}}$

Paramètres	liaisons	axe
θ	$(x_{1}, x_{2}) = θ_{2}$	$\vec{z_{1}}$
d	$x_{1} / x_{2} = 0$	$\vec{z_{1}}$
α	$(z_{1}, z_{2}) = 0$	$\vec{x_{2}}$
a	$z_{1} / z_{2} = l_{2}$	$\vec{x_{2}}$

Paramètres	liaisons	axe
θ	$(x_{2}, x_{3}) = θ_{3}$	$\vec{z_{2}}$
d	$x_{2} / x_{3} = 0$	$\vec{z_{2}}$
α	$(z_{2}, z_{3}) = 0$	$\vec{x_{3}}$
a	$z_{2} / z_{3} = l_{3}$	$\vec{x_{3}}$

Calcul des matrices de Denavit-Hartenberg

Voici les matrices déduite des 3 tableaux précédents

$M_{1} = [\begin{matrix} \cos (θ_{1}) & 0 & \sin (θ_{1}) & l_{1} \cos (θ_{1}) \\ \sin (θ_{1}) & 0 & - \cos (θ_{1}) & l_{1} \sin (θ_{1}) \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]$

$M_{2} = [\begin{matrix} \cos (θ_{2}) & - \sin (θ_{2}) & 0 & l_{2} \cos (θ_{2}) \\ \sin (θ_{2}) & \cos (θ_{2}) & 0 & l_{2} \sin (θ_{2}) \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]$

$M_{3} = [\begin{matrix} \cos (θ_{3}) & - \sin (θ_{3}) & 0 & l_{3} \cos (θ_{3}) \\ \sin (θ_{3}) & \cos (θ_{3}) & 0 & l_{3} \sin (θ_{3}) \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]$

On rappel que :

$\cos (a + b) = \cos (a) \cdot \cos (b) - \sin (a) \cdot \sin (b)$
$\sin (a + b) = \cos (a) \cdot \sin (b) - \cos (b) \cdot \sin (a)$

Calcul de la matrice $M_{23} = M_{2} M_{3}$

$M_{23} = [\begin{matrix} \cos (θ_{2} + θ_{3}) & - \sin (θ_{2} + θ_{3}) & 0 & l_{3} \cos (θ_{2} + θ_{3}) + l_{2} \cos (θ_{2}) \\ \sin (θ_{2} + θ_{3}) & \cos (θ_{2} + θ_{3}) & 0 & l_{3} \sin (θ_{2} + θ_{3}) + l_{2} \sin (θ_{2}) \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]$

Calcul de la matrice $M = M_{1} M_{2} M_{3}$

$M = [\begin{matrix} \cos (θ_{1}) \cos (θ_{2} + θ_{3}) & - \cos (θ_{1}) \sin (θ_{2} + θ_{3}) & \sin (θ_{1}) & \cos (θ_{1}) \cdot (l_{3} \cos (θ_{2} + θ_{3}) + l_{2} \cos (θ_{2}) + l_{1}) \\ \sin (θ_{1}) \cos (θ_{2} + θ_{3}) & - \sin (θ_{1}) \sin (θ_{2} + θ_{3}) & - \cos (θ_{1}) & \sin (θ_{1}) \cdot (l_{3} \cos (θ_{2} + θ_{3}) + l_{2} \cos (θ_{2}) + l_{1}) \\ \sin (θ_{2} + θ_{3}) & \cos (θ_{2} + θ_{3}) & 0 & l_{3} \sin (θ_{2} + θ_{3}) + l_{2} \sin (θ_{2}) \\ 0 & 0 & 0 & 1 \end{matrix}]$

Par Jérémy HERGAULT, le 1 octobre 2013.

Étude mécanique robot PhantomX AX Mark II

Chaine cinématique d’une patte

Calcul du système de référence

Calcul des matrices de Denavit-Hartenberg